Необходимость определять направление поездки очевидно для каждого, кто увлекается Фэн Шуй и Ци Мэнь. Нам хочется знать, например, где находится желтая пятерка месяца или года, чтобы не получить плохую ци в пути, или нужно найти правильное направление для активизации хорошей структуры.
Мы все привыкли определять расстояние и направление движения по карте, которая отображает земной шар на плоскости. Для этого мы находим две точки: начальную и конечную, проводим прямую, определяя тем самым кратчайшее расстояние на плоскости между этими двумя точками и далее смотрим направление, с учетом того, что север у нас всегда сверху карты, а юг – снизу.
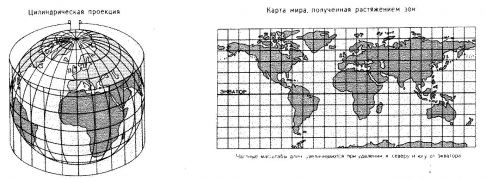
Из этого рисунка становится видно, что чем дальше от экватора, тем сильнее искажения расстояний, так как сферическая поверхность при проецировании на плоскость будет растягиваться. Чем дальше от экватора, тем сильнее растяжение. Поэтому, чем дальше расстояние, на которое мы едем, тем сложнее правильно определить направление и расстояние по карте, так как в действительности ехать мы будем не по прямой линии, а по дуге. Сначала поговорим о том, как найти кратчайшее расстояние от одной точки до другой на шаре. Для этого придется попробовать представить себе нашу Землю из космоса и расположенные на ней две точки нашего маршрута, а также вспомнить уроки геометрии уровня 10 класса общеобразовательной школы.
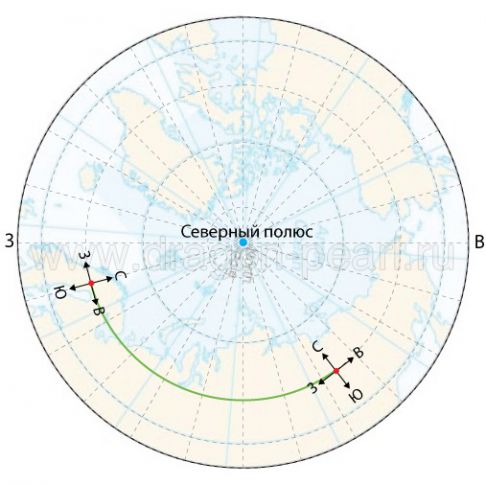
На первом рисунке мы видим две точки маршрута, расположенные на одной широте (для упрощения). И нам кажется, что, двигаясь по широте, мы двигаемся по кратчайшему пути. Но это – на плоской карте. На соседнем рисунке изображен тот же маршрут, но уже в 3D – глядя на земной шар со стороны Северного полюса. И тут обнаруживается, что мы можем найти более короткий путь, но он пролегает не по широте.
Чтобы это понять, мы должны вспомнить, что земля – это шар, и применить знания геометрии, чтобы найти кратчайшее расстояние между точками на шаре.
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками, находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии кратчайшее расстояние между двумя точками – прямая линия. На сфере прямых линий не бывает. Все линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы. 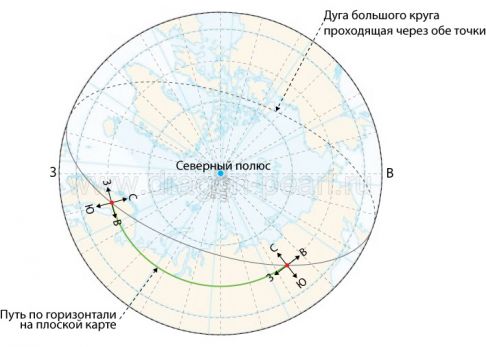
Из описания и рисунка нам становится понятно, что, когда мы ходим на небольшие расстояния, мы двигаемся практически по плоскости, но когда расстояния становятся большими – мы уже двигаемся по сфере, где маршрут становится не прямой линией, а дугой, у которой есть начальный вектор движения и конечный вектор, называемые азимутами. Теперь мы видим, что движение вдоль широты не является кратчайшей траекторией. Мы движемся по дуге, и это движение может существенно отличаться от спроецированного на плоскую карту. И тут мы плавно переходим к определению направления.
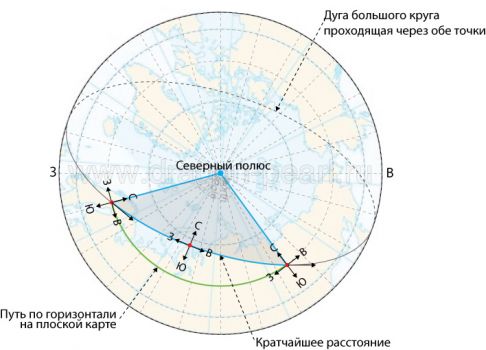
Начальный и конечный угол (азимуты) на нашем кратчайшем пути различаются. У нас есть север и юг, местоположение которых определяется полюсами. При движении строго с севера на юг или обратно, если мы движемся по линии меридиана, искажение азимута направления не происходит. А вот если мы отправляемся в путь, пересекая меридианы, азимут «прилета» (конечной точки) может существенно отличаться от азимута «отлета». Как мы видим на рисунке ниже, вылетая на северо-восток, мы можем легко прилететь на юго-восток. Причем чем ближе к полюсам, тем искажения сильнее, и тем сильнее реальные направления отличаются от направлений на карте. Если же наши точки расположены на линии экватора, то азимуты «отлета» и «прилета» не будут противоречить друг другу.
Особенно нагляден пример, когда конечная точка находится на той же параллели, что и точка старта, но на противоположном конце земного шара. Тогда, вылетая на север, мы, по сути, прилетаем на юг.
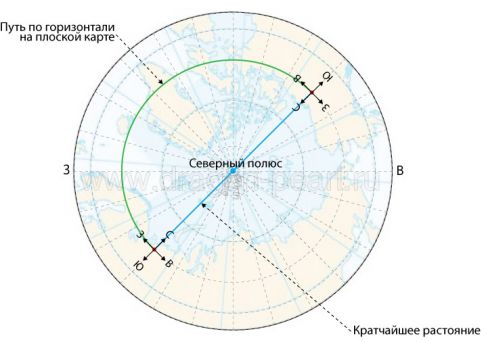
Если переводить все рассуждения на плоскость выбора направления, можно резюмировать так. Если вы практикуете в рамках школы, для которой важен первоначальный вектор движения, то смотрите азимут отбытия. Например, для полета из Москвы в Сингапур азимут вылета (без учета магнитного склонения) – 108°54 (восток), а азимут прилета 147°89 (юго-восток). Однако помните, что самолеты не всегда летят по кратчайшему пути; для их передвижений существуют воздушные коридоры, и может оказаться, что отправляясь на юго-восток, вы сначала полетите, например, на юг или восток. Для того, чтобы ориентироваться по азимуту отлета, вам надо хорошо знать небесные маршруты.
Если же вас интересует направление конечной точки путешествия, то вам нужен азимут прибытия. Именно он определяет направление, в котором мы прибываем, то есть завершение нашего пути, направление конечной точки. Для большинства технологий важна именно она.
Рассчитать направления для своих путешествий вы сможете на сайте www.mingli.ru в разделе Навигатор.
Приятного и полезного пути!








 Константин Воркунов
Константин Воркунов


Здравствуйте, Наталья! Извините за сотый вопрос по этой теме, пытаюсь тоже разобраться, если не тяжело, объясните, почему москва-нью-йорк - это юго-запад, а москва -сиэтл это юг, если разница в широте между нью-йорком и сиэтлом в 7 градусов, нью-йорк даже южнее. По отношению к Москве Сиэтл западнее по сравнению с Нью-Йорком, но не южнее. Пытаясь разобраться я даже просматривала программу google earth, где наша планета т.с. в реальном виде представлена. Но так и не поняла, почему сиэтл это юг, а нью-йорк ЮЗ. Я не имею в виду вылетели в север прилетели в юг, я беру место прибытия. Азимут вылета и магнитное склонение отключаю.
Спасибо.